[Deep Learning] AutoEncoder (AE)

이번 포스팅에서는 AutoEncoder에 대해서 다루어보도록 하겠습니다. (AutoEncoder에 대한 자료를 찾아보신 분들은 한번씩은 접하는 끝판왕급 자료 이활석님의 "오토인코더의 모든것". 저도 많이 참고하였습니다. 링크를 원하는 분은 여기로 접속하시면 됩니다)

 

AutoEncoder (AE)

AutoEncoder는 통상적으로 아래와 같은 구조를 갖는 Feed-Forward Neural Network를 지칭합니다.

Reference: Hands on Machine Learning; https://github.com/ExcelsiorCJH/Hands-On-ML/blob/master/Chap15-Autoencoders/Chap15-Autoencoders.ipynb

앞 단의 인코더(Encoder)로 들어가서 중간 bottleneck layer를 통과하여 다시 인코더(입력)와 같은 크기의 디코더(출력)이 나오는 구조이구요. 예를들어 고양이 사진을 넣어서 네트워크를 통과시킨 후 다시 이 고양이 사진을 복구시키는 Task가 Auto-Encoder를 사용하는 상황이라고 보시면 됩니다. 이런 방식으로 input 자기 자신을 학습시키기 때문에 오토인코더는 semi-supervised learning 방법론으로 볼 수 있을 것 같습니다(신경망구조는 label이 필요한 supervised learning 방식이지만 추가적인 label을 넣는 것이 아니라 자기 자신을 넣기 때문에 실질적으로는 unsupervised learning이나 마찬가지라는 것이죠). 

 

자, 그럼 대체 왜 자기 자신을 다시 복구하는 네트워크를 만드는가? 그것이 AutoEncoder의 핵심입니다.

우리가 피상적으로 획득하는 고차원의 관측치들은 뭔가 감춰진(?) 저차원의 기저 요인(Latent/hidden Variable)에 의해서 발현되는데, AutoEncoder 구조를 활용하면 그러한 중요한 요인들을 잡아낼 수 있다는 컨셉입니다. 구조적으로 보자면 오토인코더의 bottleneck layer에서 이러한 잠재요인들을 압축적으로 뽑아내게 됩니다. 이 컨셉을 어려운 표현으로는 Manifold Hypothesis라고 하는데요, 

• Natural data in high dimensional spaces concentrates close to lower dimensional manifolds
• Probability density decreases very rapidly when moving away from the supporting manifold 

 

요게 무슨말인지는 이활석님이 설명해주신 예시에서 직관적으로 이해할 수 있습니다. MNIST 데이터를 보면

Reference: https://programmer.ink/think/building-mnist-handwritten-number-recognition-with-keas-and-tensorflow.html

보시는 그림에서 28X28개의 픽셀 하나하나가 input feature가 됩니다. 픽셀 하나가 가질 수 있는 밝기 값은 0~255입니다. 실제 어떤 MNIST 샘플들이 있는지에 대한 생각은 잠시 접어두고 "이론적으로" 이 상황에서 나올 수 있는 샘플의 가짓수는 몇 개나 될까요? 28X28X256 가지입니다. 픽셀이 28X28개가 있는데 (맨구석에 위치한 픽셀이든 중앙쪽에 위치한 픽셀이든) 각각의 픽셀이 가질수 있는 값은 256가지니까요. 그럼 우리가 실제로 표집하게 되는 샘플은 보통 어떤 모양이죠? 

사실 실제 데이터에서는 밝은 픽셀이 전 위치에 골고루 퍼져있지 않습니다. 구석에 있는 픽셀은 대개 값이 0이라고 보시면 되고, 중앙에 있는 픽셀들이 label에 따라 조금씩 변화하죠. 다시 표현하면 관측치들이 Feature Space 전 공간에 골고루 퍼져있지 않고 특정한 국소공간에 밀집되어 있다는 말입니다. 만약에 실제 데이터가 Feature Space에 골고루 퍼져있었다면, 우리가 Feature space에서 Feature값을 무작위로 할당해서 임의의 sample을 만들어냈을 때 만들어진 sample이 실제 관측 sample과 유사할 것입니다. 그렇지만 28X28 픽셀 이미지를 무작위로 생성하면 대개 아래 보시는 것과 같은 이미지가 만들어지죠. 전혀 실제 MNIST sample과 비슷하지 않습니다.

 

이러한 가설하에서는 의미있는 데이터가 밀집되어 있는 Manifold를 알아내서 학습하는 것이 목적이 되는 것입니다. 아래 예시에서는 3차원 Feature space가 나타나있고, 그 Feature space에서 실제 데이터가 밀집되어 있는 부분집합, Manifold가 2차원 나선형 구조로 나타나 있습니다. 

바로위에서 우리가 무작위로 만들어 낸 샘플은 실제 데이터가 밀집되어 있는 나선 구조위에 존재하는 것이 아닌 그 외의 바깥지역에 존재할 것입니다.

 

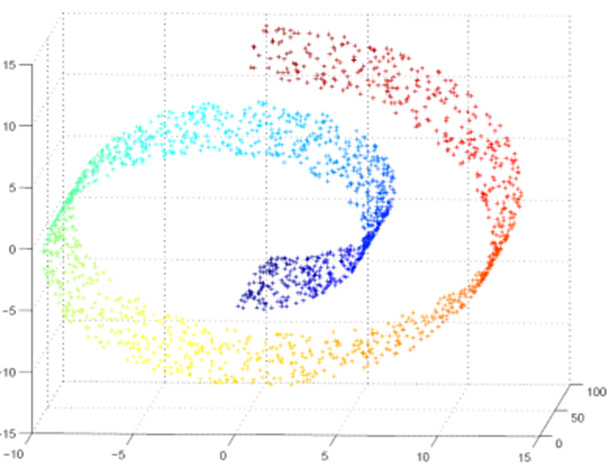
'어차피 Feature space가 품고 있는 부분집합인데 굳이 Manifold를 찾아야 하나?' 라고 생각하실 분들도 계실 겁니다. 

 

좀 더 직관적인 이해를 위해 이활석님의 아래 예시를 볼까요?

우리가 보기에는 의미적으로 가깝다고 생각되는 두 샘플들 간 거리가 고차원 Feature space에서는 먼 경우가 있다는 겁니다. 거꾸로 고차원 공간에서 가까운 데이터 포인트들이 의미적으로는 별로 유사하지 않을 수 있구요. 

 

위 그림에서 첫번째 사진과 세번째 사진을 봅시다. 골프공을 때리는 순차적인 사진이라고 쉽게 추론가능한데요, 이 두 사진의 중간 단계사진은 어떻게 될까요? 실제로는 골프채를 그 첫번째와 세번째 중간 어디쯤에 들고 있는 사진이 되어야할 겁니다. 하지만 Feature space에서 중간지점(평균)을 찾으면 어떻게 되나요(첫번째 이미지와 세번째 이미지를 합쳐서 평균을 내면 Feature space에서의 중간지점입니다)? 막 손이 세개 네개 나오는 사진이 됩니다. 실제로는 나올수가 없는 사진. 왜냐하면 실제 데이터가 존재하는 manifold 상의 위치가 아니기 때문에 실존하지 않는 이상한 관측치가 나온 것입니다. 제대로 하려면 manifold 상에서의 중간지점을 찾아야 한다는 겁니다. 

manifold를 찾아 그 manifold에서의 중간지점을 찾으면 보시는 바와 같이 골치를 그 중간 어디쯤 들고있는 실제와 유사한 output이 도출되게 됩니다. 

 

이러한 맥락을 이해하면 왜 AE(Auto-Encoder)가 데이터 압축이나 이상탐지에 활용되는지도 눈치채실 수 있을 겁니다. 때문에 고전통계기법 중에 PCA(Principal Component Analysis)와 자주 비견되는 방법론이기도 합니다. (PCA에 대한 포스팅은 추후 업로드 하도록 하겠습니다... 쓰고 싶은 포스팅은 많으나 글 하나 작성하는데 시간이 꽤 많이 드네요 ㅜㅜ)

이것으로 포스팅을 마치겠습니다.