그러면 이제 ARIMA 모델링을 적용하는 표준 절차에 대해서 한번 살펴볼까요? Box-Jenkins의 ARIMA procedure입니다.
1. 모델 식별 (Model Identification)
시계열이 stationary인지 체크하고 그렇지 못할 경우 추세/주기성 제거, 차분, 시계열 변환 등을 활용해서 시계열을 안정화하는 작업을 선행합니다(ARIMA모델의 차수 \(d\) 는 시계열의 차분 횟수를 의미합니다). 여기서, 비정상 시계열을 정상화하는데 만능키처럼 차분을 남용하는 것은 좋지 않습니다. 기본적으로 차분이라는 것은 정보를 꽤나 많이 손실시키는 작업이기 때문에(예를 들어서 상수항의 의미도 '절편'에서 '기울기'로 달라지죠) 최대한 다른 처리를 통해 정상화를 시도해보고 최후의 보루로서 시도하는 것이 좋습니다.
이렇게 안정화 된 시계열을 ARIMA 모델에 적용할 때 적절한 차수를 설정합니다.
\(p\) : Autoregressive 항의 차수
\(d\) : 차분 차수
\(q\) : Moving Average 항의 차수
ARIMA모델은 이 차수를 결정하면 ARIMA(p, d, q)와 같은 식으로 표기합니다.
\[ \Phi_p(L) (1 - L)^d Y_t = \Theta_q(L) \epsilon_t \]
2. 모델의 추정 (Model Estimation)
최소자승법(Least Squares Method) 혹은 최우도추정법(Maximum Likelihood Estimation, MLE)를 활용하여 모델의 parameter를 추정합니다.
3. 모델의 진단 (Model Diagnostics)
모델의 적합성과 정확성을 검정합니다. 모델이 시계열 데이터를 적절히 설명하는지 확인하고, 필요하면 모델을 수정합니다. 기본적으로 모델로부터 나오는 잔차(residuals)는 white noise여야 합니다. 우리가 시계열에서 최대한 정보를 쪽쪽 빨아내고 거의 정보가 없는 녀석만 남아야 하는 것이죠. 만약 잔차분석 등에서 문제가 발견되면 다시 전 단계로 돌아가서 ARIMA 차수를 조절하고 모델을 수정하는 작업을 반복합니다.
모델의 정상성 그리고 차수를 결정하는데 중요한 역할을 하는 것이 자기상관함수(ACF), 편자기상관함수(PACF) 입니다. 그 전에도 언급이 나왔던 것 같은데 이번 기회에 한번 정리하고 넘어가겠습니다.
1. 자기상관함수 (Autocorrelation function, ACF)
시계열 데이터의 자기상관을 시차(lag)에 따라 측정한 함수입니다. \(k=0\)일 때 ACF는 항상 1입니다.
\[ \rho_k = \frac{\text{Cov}(Y_t, Y_{t-k})}{\sqrt{\text{Var}(Y_t) \cdot \text{Var}(Y_{t-k})}} = \frac{\sum_{t=k+1}^{T} (Y_t - \bar{Y})(Y_{t-k} - \bar{Y})}{\sum_{t=1}^{T} (Y_t - \bar{Y})^2}, \]
\(Y_t\): 시계열 데이터
\(k\): 시차(lag)
\(\bar{Y}\): 데이터의 평균
\(T\): 데이터의 총 길이
2. 편자기상관함수 (Partial Autocorrelation Function)
PACF는 특정 시차에서 다른 시차의 영향을 제거한 자기상관을 측정합니다. 즉, \(k\)시차에서의 PACF는 \(k-1\)까지의 시차 효과를 제거한 순수 \(k\)시차의 영향입니다. 아래 수식은 Durbin-Levinson의 알고리즘을 활용한 PACF계산 방법입니다.
1. 초기화 (\(k=1\))
\[ \phi_{11} = \rho_1 \]
2. 재귀 관계 (\(k \geq 2\))
\[ \phi_{kk} = \frac{\rho_k - \sum_{j=1}^{k-1} \phi_{k-1,j} \rho_{k-j}}{1 - \sum_{j=1}^{k-1} \phi_{k-1,j} \rho_j} \]
- 비정상 시계열의 경우에는 ACF가 매우 천천히 감소하는 모양을 띱니다. 반면에 정상시계열은 빠르게 ACF가 0으로 가까워집니다.
- ARIMA의 차수는 다음과 같은 기준으로 정할 수 있습니다(물론 정량적인 기준이 있는 것은 아니기에 주관적기준이죠).
| Model | ACF | Partial ACF |
|---|---|---|
| MA(\(q\)) | Cut off after lag \(q\) (\(q\) 시차 이후 0으로 수렴) |
Die out (지수적으로 감소/소멸하는 sine 함수 형태) |
| AR(\(p\)) | Die out (지수적으로 감소/소멸하는 sine 함수 형태) |
Cut off after lag \(p\) (\(p\) 시차 이후 0으로 수렴) |
| ARMA(\(p, q\)) | Die out (시차 (\(q+p\)) 이후부터 소멸) |
Die out (시차 (\(q+p\)) 이후부터 소멸) |
시뮬레이션 데이터(ARIMA(1,1,0))를 통해서 파이썬에서 ARIMA를 적용하는 과정을 연습해볼까요?
# Import necessary libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
# Step 1: Generate synthetic ARIMA(1,1,0) data
np.random.seed(42)
n = 200
phi = 0.7 # AR coefficient
noise = np.random.normal(0, 1, n)
# Generate ARIMA(1,1,0) data
y = np.zeros(n)
for t in range(1, n):
y[t] = y[t - 1] + phi * (y[t - 1] - y[t - 2] if t > 1 else 0) + noise[t]
# Convert to pandas Series
ts_data = pd.Series(y, name="ARIMA(1,1,0)")
# Plot the original data
plt.figure(figsize=(10, 5))
plt.plot(ts_data, label="ARIMA(1,1,0) Data")
plt.title("Simulated ARIMA(1,1,0) Time Series")
plt.legend()
plt.show()
# Step 2: Perform Augmented Dickey-Fuller (ADF) Test
def adf_test(series):
result = adfuller(series)
print("ADF Statistic:", result[0])
print("p-value:", result[1])
print("Critical Values:", result[4])
if result[1] < 0.05:
print("The data is stationary.")
else:
print("The data is non-stationary.")
print("ADF Test for Original Data:")
adf_test(ts_data)
# Step 3: Differencing to Make Data Stationary
ts_diff = ts_data.diff().dropna()
# Plot Differenced Data
plt.figure(figsize=(10, 5))
plt.plot(ts_diff, label="Differenced Data")
plt.title("Differenced Time Series")
plt.legend()
plt.show()
print("ADF Test for Differenced Data:")
adf_test(ts_diff)
# Step 4: ACF and PACF Plots
plt.figure(figsize=(10, 5))
plot_acf(ts_diff, lags=20, title="ACF of Differenced Data")
plt.show()
plt.figure(figsize=(10, 5))
plot_pacf(ts_diff, lags=20, title="PACF of Differenced Data")
plt.show()
# Step 5: Fit ARIMA(1,1,0) Model
model_110 = ARIMA(ts_data, order=(1, 1, 0))
fitted_model_110 = model_110.fit()
# Print Model Summary
print(fitted_model_110.summary())
# Step 6: Forecast Future Values
forecast_110 = fitted_model_110.forecast(steps=12)
# Plot Forecast
plt.figure(figsize=(10, 5))
plt.plot(ts_data, label="Original Data")
plt.plot(range(len(ts_data), len(ts_data) + 12), forecast_110, label="Forecast", color="red")
plt.title("ARIMA(1,1,0) Model Forecast")
plt.legend()
plt.show()
일단 원 시계열을 먼저 살펴볼까요? 딱 봐도 Stationary는 아닌것 같긴합니다.
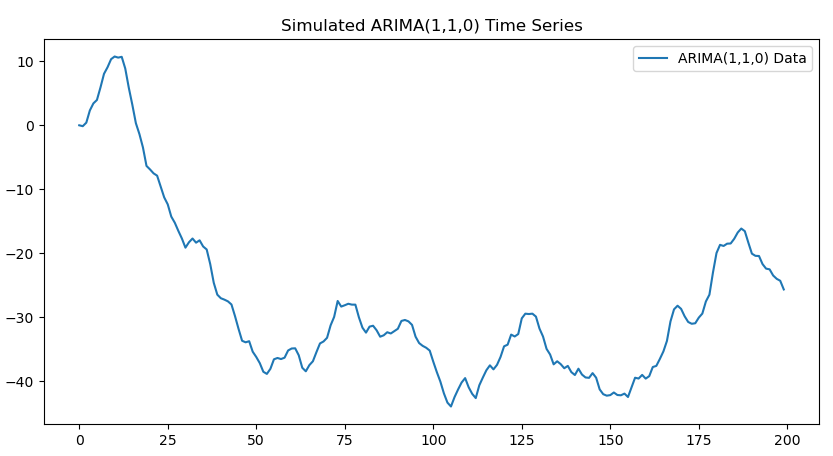
ADF 테스트를 해볼까요?
ADF Test for Original Data:
ADF Statistic: -2.1952124040709213
p-value: 0.2079876646010212
Critical Values: {'1%': -3.4638151713286316, '5%': -2.876250632135043, '10%': -2.574611347821651}
역시나 비정상시계열이고 Unit root이 존재하는 것으로 보이기에 차분을 진행합니다.

그럼 Box-Jenkins의 프로시져에 따라 ACF와 PACF를 한번 봐볼까요?


PACF는 1 이후 뚝 끊겨버리고 ACF는 지수적으로 감소하는 모양이네요. 차분한 시계열이 AR(1)로 의심(!?)됩니다. 그래서 이 차수로 ARIMA 분석을 수행후 미래를 예측해보면 다음과 같습니다.

Box-Jenkins 프로시져는 말씀드린바와 같이 주관적 기준이라는 한계가 있기 때문에 나름대로 객관화된 기준을 위해 AIC, BIC등의 지표로 p, d, q차수를 지정하기도 합니다(python의 Auto-arima 등). 하지만 시계열 분석의 어려운 점은 항상 통용되는 솔루션이 없다는 점입니다. 여러 정보를 취합하여 종합적으로 판단은 내려주어야 한다는 점 기억하시기 바랍니다.
'Data & Research' 카테고리의 다른 글
| [ML & DL 기초] Table of Contents (1) | 2025.03.15 |
|---|---|
| [Time series] Table of Contents (0) | 2025.02.26 |
| [Time series] 시계열의 정상화 (2) | 2025.01.11 |
| [Time Series] ARMA parameter의 MLE 추정 (2) | 2024.11.30 |
| [Time Series] ARMA Forecast (2) | 2024.11.27 |