1. Reject Sampling (Accept-Reject Sampling)
알고리즘은 아래와 같습니다. 아래 블로그에서 퍼왔습니다.
https://untitledtblog.tistory.com/134
[머신 러닝] 기각 샘플링 (Rejection Sampling)
Rejection sampling (또는 acceptance-rejection method)은 어떠한 주어진 확률 분포에서 효율적으로 샘플을 생성하기 위해 많이 이용되는 알고리즘이다. 우리가 샘플을 추출하고자 하는 확률 분포 $p$에 대
untitledtblog.tistory.com

우리가 어떤 분포를 알고는 있으나 그 분포로부터 샘플을 추출하고자 할 때 사용합니다. 샘플링의 대상이 되는 분포는 p, 그 분포에서의 샘플링에 동원되는 함수를 q라고 하고 Mq가 p를 충분히 감쌀 수 있을 만한 상수 M를 설정합니다. M은 되도록 작으면 좋겠죠? q에서 샘플을 뽑되, 뽑힌 샘플을 모두 다 쓰는 것이 아니고 p분포와 Mq분포의 확률을 고려하여 확률적으로 accept/reject하는 과정을 거칩니다. 확률분포가 넓게 퍼져있는 경우에는 reject 해야하는 샘플이 너무 많아서 비효율적입니다.
2. Importance sampling
Reject 샘플링은 위에서 말씀드린 단점이 있는데요, 우리가 분포를 구하는 목적이 대부분 기대값 계산을 하기 위함이죠. 그럼 그 목적을 위한 좀 더 적절한 방법을 찾을 수는 없을까요? 그게 importance sampling입니다. 알고리즘은 아래와 같습니다. (위 블로그와 동일한 블로그에서 퍼왔습니다)

우리가 target으로 하는 확률분포 p(x)에 관한 기대값을 구하고자 할 때, importance sampling으로 효율적인 기대값 연산을 할 수 있습니다.


원래 구하고자 하는 값의 분산과 샘플링을 이용하여 구한 분산은 아래와 같습니다(샘플링해서 구할 때 원래 분산보다 커질수도 있다는 점을 확인할 수 있습니다. 결국 이 부분이 단점이라고 할 수 있겠습니다).
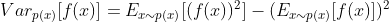

3. Markov Chain Monte Carlo (MCMC)
드디어 궁극적인(?) 목표인 MCMC에 대해서 이야기할 때가 왔습니다. 다만 그 전에 Markov Chain에 대해서 먼저 살펴보겠습니다. Markov Chain의 정의를 위키피디아에서는 이렇게 말하고 있습니다.
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event
아 네... 그렇군요. 이해하기 예시를 들어서 이해해볼까요? 원자는 들뜬상태와 바닥상태가 있...
OTT 서비스 업체 2군데만 있다고 해봅시다. Netflix와 Watcha 뿐이에요 (티빙, 디즈니 등등 기타 서비스 이용자분들 죄송합니다). 우리는 이번달 넷플릭스를 구독했던 사람이 다음달도 구독할 확률은 얼마나 되는지, 왓챠로 이동할 확률이 얼마나 되는지(거꾸로 왓챠에선 어떤지) 이런 확률들을 알아내고 싶습니다.

지금 위에서 보시는 그림에서의 전이(trainsition) 확률들을 알아내고 싶은 겁니다. 그런데, Markov Chain의 상당히 강한 가정이 있습니다. 이런 전이 확률이 바로 직전의 '상태'에만 의존해서 확률적으로 결정된다는 것입니다. 즉, 이번달 어느 플랫폼 구독할 것인지 여부는 전적으로 "지난달 어떤 서비스를 구독했었니?"에만 의존한다는 것입니다. 그런데, 실상은 그렇지 않죠? 우리는 상태 외적인 부분에 영향을 받기도 하고(넷플릭스에서 '킹덤'이나 '오징어게임'을 출시했다면 영향을 받죠), 전월 이전의 정보에 영향를 받기도(넷플릭스를 6개월 구독했더니 슈츠도 다보고 볼게 별로 없네) 합니다. 물론 다른 모형들이 다 그렇듯이 이런 가정을 완화하기 위한 발전된 Markov 계열의 모형들이 나오긴 했지만 어쨌든 Markov 모형의 기본 철학은 이와 같습니다. 이런 가정을 하게되면 처음에 얼마나 많은 사람이 넷플릭스/왓차에 있었든 시간이 흐르고 나면 넷플릭스 구독자와 왓챠 구독자 비율은 일정한 값에 수렴하게 되고(stationary) 각 전이 확률을 계산할 수가 있습니다. Markov 모형에 대한 시뮬레이션은 아래 웹페이지를 참고하시면 좋을 것 같습니다.
https://towardsdatascience.com/markov-chain-analysis-and-simulation-using-python-4507cee0b06e
Markov Chain Analysis and Simulation using Python
Solving real-world problems with probabilities
towardsdatascience.com
이제 MCMC의 앞 부분은 해결이됐구요, Monte Carlo기법은
몬테카를로 방법(Monte Carlo method) (또는 몬테카를로 실험)은 반복된 무작위 추출(repeated random sampling)을 이용하여 함수의 값을 수리적으로 근사하는 알고리즘을 부르는 용어이다
라고 위키피디아가 알려줍니다. 위키피디아에는 아래 예시는 확인할 수가 있는데요, 원주율(phi)의 값을 sampling을 통해 수치적으로 계산하는 과정을 보여줍니다. 원의 공식을 이용하면 사분원의 넓이는 phi/4가 될텐데 사분원을 포함하고있는 사각형의 넓이는 1입니다. 그러니까 이 사각형에 무작위로 점을 흩뿌려서 (사분원 안에 들어있는 점의 개수) X 4 / (사각형 안에 들어있는 점의 개수) 를 계산해주면 phi값을 수치적으로 획득할 수 있는 것입니다. 이러한 접근법을 몬테카를로 방법이라고 하는 것이구요.

자, Markov Chain과 Monte Carlo method를 모두 알아보았으니 드디어 MCMC에 대해 알아볼 차례입니다!
앞선 Reject/Importance sampling은 샘플링 각각이 모두 독립적이라고 생각합니다. 수렴 속도가 일반적으로 느립니다. MCMC는 샘플링 과정에서 Markov Chain 을 통해 이전 샘플링 정보를 활용합니다. stationary 분포로 나아가는 transition rule을 찾아내는 것이 MCMC의 목적이라고 할 수 있습니다.

1) Metropolis-Hastings Algorithm
대표적인 MCMC알고리즘인 Metropolis-Hastings 알고리즘에 대해서 알아볼까요?

Metropolis 알고리즘에서 trainsition matrix가 symmetric하지 않은 경우로 일반화시킨 것이 Metropolis-Hastings 알고리즘입니다. 그것을 위해서 원래 Metropolis M-ratio에 추가적인 보정항이 들어간 것을 확인하실 수 있습니다.
샘플링의 구체적 예시 상황은 아래 블로그에서 참고하세요
https://angeloyeo.github.io/2020/09/17/MCMC.html
Markov Chain Monte Carlo - 공돌이의 수학정리노트
angeloyeo.github.io
2) 깁스 샘플링 (Gibbs sampling) : Metropolis-Hastings 알고리즘의 special case
일단 깁스 샘플링의 가장 큰 특징은 proposal distribution을 새로운 것으로 잡지 않고 재활용하겠다는 것입니다. 이와 같은 방식으로 Markov Chain의 detailed equation을 자동만족시킬 수 있습니다(alpha를 통해 받아들일지 기각할지 보정하는 작업을 하지 않아도 됩니다). 또 추정하고자 하는 모수가 다변수일 때 각 변수 업데이트 시 다른 변수들을 모두 고정시켜두고 업데이트 한다는 점도 특징입니다. detailed equation 충족에 대한 증명은 아래 블로그를 참고하세요
https://rooney-song.tistory.com/28
깁스 샘플링(Gibbs sampling)
깁스 샘플링(Gibbs sampling)에 대해 알아볼 것이다. 다룰 내용은 다음과 같다. 1. 깁스 샘플링 2. 깁스 샘플링의 예제 1. 깁스 샘플링 깁스 샘플링은 Metropolis Hastings(이하 MH) 알고리즘의 특별한 형태로,
rooney-song.tistory.com
사실 이론만으로는 이해가 좀 어려울 수도 있는데, 샘플링을 활용하는 구체적 사례에 대해서 포스팅을 더 추가하도록 하겠습니다.
'Data & Research' 카테고리의 다른 글
| [Deep Learning] Convolutional Neural Network (CNN) (0) | 2021.11.16 |
|---|---|
| [Machine Learning] 모델의 평가 (0) | 2021.11.14 |
| [Statistics] 베이지안 통계학 (Frequentist vs. Bayesian) (0) | 2021.11.07 |
| [Statistics] 나이브 베이즈 (Naïve Bayes) (0) | 2021.11.06 |
| [Machine Learning] 앙상블(Ensemble) 기법 (1) | 2021.11.06 |



