이번 포스팅에서는 통계학의 두 학파 빈도주의(Frequentist)와 베이지안(Bayesian)에 대해서 알아보겠습니다. 우리가 기본 교과 과정을 통해 기본적으로 습득한 관점이 빈도주의 기반 관점이라고 보시면 되구요. 그럼 베이지안이 어떤 관점인지 한 번 알아볼까요? (베이지안 관점은 칼만필터, Bayesian deep learning 등에 적용되고 있죠)
베이지안 관점에서는 구하고자 하는 모수가 '고정된 값'이 아니라 분포가 되고, 때문에 hyper-parameter가 관여하게 됩니다. 하지만 무엇보다 중요한 핵심은 "우리의 선험적 지식"을 반영하여 "보정" 작업을 한다는 것이 가장 큰 차이일 겁니다. (이 때문에 빈도주의자들에게서 이거 일종의 조작 아니냐?는 비판을 받는 것이기도 하구요)
여기까지 이야기만으로는 잘 와닿지 않으실 수 있으니 동전 던지기 예시를 통해 이해해볼까요? 동전을 던지는 사건을 보통 베르누이(Bernoulli) 분포로 근사하고 여러번 던졌을 때 앞면이 나오는 횟수는 이항(Binomial)분포로 근사합니다. 이 때, 5번 동전을 던져서 앞면이 1번 나왔다고 해볼까요? 그럼 빈도주의 관점에서 최우도추정을하면 앞면이 나올 확률은 얼마가 될까요? 아주 직관적인 결과 즉, 앞면이 나올 확률이 1/5이 됩니다. 과거관측에서 앞면의 빈도가 곧바로 추정된 확률입니다. (물론 모든 추정문제에서 이렇게 직관적으로 이해하기 쉬운 결론이 나는것은 아닙니다만 예시는 이해하기 쉬울수록 좋으니까요. 자세한 수식전개는 아래 블로그를 참고하세요)
http://norman3.github.io/prml/docs/chapter02/1.html
1. Binary Variables
1. Binary Variables 우선 가장 간단한 형태의 식으로 부터 논의를 시작한다. 랜덤 변수 \( x \) 가 \( x \in \{ 0,1 \} \) 인 상황(즉, 취할 수 있는 값이 단 2개)에서의 확률 분포를 살펴본다. 가장 간단한 경
norman3.github.io
이 빈도주의 관점의 결론에 대해 여러분은 불만이 없으신가요? 만약 5번의 시행에서 모두 뒷면이 나왔더라도? (이 경우라면 최우도추정에서 앞면이 나올 확률은 0/5=0 입니다) 베이지안들이 이 맥락에서 등장하는 거죠. "아니 우리의 직관적인 판단에 따르면 동전 던졌을 때 앞면/뒷면 모두 나올 수 있는 것이 타당한데, (특히나 관측치의 개수가 적은 상황에서) 앞면이 안나왔다고 그 확률을 깡그리 무시하는게 말이되느냐" 이겁니다.
이러한 주장도 타당한 측면이 있습니다. 시행을 100번, 1000번 한다면 앞면이 한번도 나오지 않을 확률은 극히 미미하겠지만, 시행 횟수가 작을 경우에는 앞면이 나올 확률이 있더라도 관측이 안될 확률이 꽤 있으니까요(예를들어 앞면이 나올 확률이 1/2이라고 해도 5번 다 나오지 않을 확률은 1/32입니다. 낮긴하지만 그렇다고 세상에 그런일은 있을 수 없다고 단언할 정도는 아니죠) 그러니까 우리의 추정을 보정해주겠다는 겁니다. 어떤방식으로? 베이즈정리를 활용해서! 먼저 베이지안 일반론을 설명드리고 동전예시로 돌아오겠습니다.
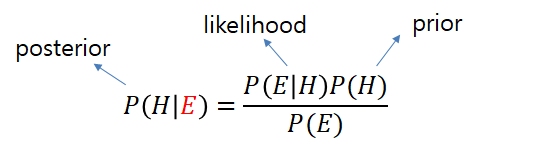
여기서 E는 관측된 정보(5번 던져서 1번째에 뒷면...5번째에 뒷면)를 H는 우리가 찾고자 하는 parameter(=앞면이 나올 확률)을 의미합니다. 원래 빈도주의 관점에서는 어떻게 추정했죠?
likelihood만을 놓고(우도:likelihood)가 최대가 되도록하는 고정된 하나의 참값 H를 찾기위해 노력합니다. 선형 회귀분석/로지스틱 회귀분석에서 최우도추정에 대한 부분을 말씀드렸었죠? 그런데 이제 H를 약간 보정해주고 싶습니다. H를 고정불변의 진실값이 있어서 그걸 찾는다고 하면 어찌 보정을 가할 도리가 없습니다. 데이터 조작을 해주지 않고서야 그 최대치를 찾는다는데 관여할 여지가 없죠.
- 그래서 H를 "고정된 값"이 아닌 "확률변수" 즉, 어떤 분포에서 튀어나오는(realization) 값으로 관점을 전환(확률변수이기 때문에 그 변수를 정확히 이해하려면 상수값을 찾는 것이 아니라 분포전체를 정확히 구해야겠죠)합니다.
- 그리고 우리가 미리 알고있는 선험적지식이 반영된 parameter H의 분포를 prior라고 하고(이 prior분포를 우리 입맛에 맞게 조절해줄 수 있는 변수들을 hyper-parameter라고 합니다) likelihood에 곱해서 같이 반영해줍니다.
- 이렇게 우도뿐아니라 선험적인 지식(보정)이 가미된 최종분포가 parameter의 사후분포(posterior)가 되는 것입니다.
정리해보면, '종전 빈도주의자들은 구하고자 하는 parameter가 고정불변의 진실값이 있다고 보고 그것을 구했는데, 베이지안들은 그 parameter 추정에 보정을 하고 싶어서 parameter를 고정불변의(상수) 값을 보지 않고 분포에서 나오는 확률변수로 간주한다. 그리고 prior 분포를 곱해주는 과정을 통해서 parameter 분포에 보정을 해준다.' 정도가 되겠습니다.
베이지안 관점에서 parameter는 상수가 아니라 확률변수 이지만 어쨌든 그 parameter분포 중에서도 추정치 하나를 내어야한다는 관점에서는 어떤 값을 제시하면 좋을까요? posterior를 최대화하는 parameter를 찾아 제시하면 되겠죠? 이게 Maximum A Posterior estimation (MAP)입니다.
동전던지기 예시로 돌아와볼까요? 수식적으로 posterior를 계산하는 것은 여기 웹페이지에 나와있습니다. 동전 N번을 던져서 앞면이 m번, 뒷면이 l번 나왔다고 하면, 동전던지기의 우도(likelihood)는 아래와 같습니다. 여기서 μ가 우리가 구하려는 parameter가 되겠죠
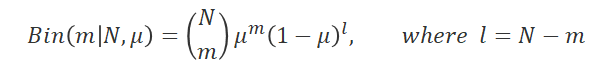
(만약 5번 던져서 모두 뒷면이었다면 m=0, l=5를 넣어야 했을 겁니다. 우도를 최대화 시키는 μ=0이 되구요) 자, 이제 우리는 우리의 선험적지식을 통해 여기에 보정을 가합니다. 보정을 가하는 분포는 베타(Beta) 분포입니다. 왜 하필 베타분포인지는 밑에서 다시 설명하겠습니다. 그리고 μ에 대한 분포를 보정한다고 했는데 정확히 어떤식으로 보정할지는 μ분포의 모양에 영향을 주는 hyper-parameter a, b에 의해 결정됩니다.

이 베타분포를 우도인 이항분포에 곱하면 사후확률이 되겠죠. (앞의 계수는 분포의 적분값이 1이되도록 하는 normalization 계수이니 생략하고 쓰겠습니다)

이제 보정이 되었죠. 아무리 앞면이 한번도 나오지 않았다하더라도 그와 관련된 항이 완전히 사라지진 않았습니다. 그런데, 한 가지 더 특이한 점이 있습니다. Posterior의 꼴이 사전확률의 꼴을 하고 있습니다.

위와 같이 a' , b'으로 치환해놓고 보면 또 베타분포가 됩니다. 여기서 다시 한 번 동전던지기를 시행한다고 하면 이제 이 posterior가 그다음번 likelihood의 prior로 작용하는 것이죠.
여기서 우리는 hyper-parameter의 의미적인 부분도 잡아낼 수 있습니다. 처음 아무정보도 없을 때는 a=b=1인 것이나 다름없어요. 그러다 N번 중에 m번은 앞면이 l번은 뒷면이 나오고 나서 정보가 업데이트 되어 a값에는 m가 더해졌고, b값에는 l이 더해졌습니다. 저 베타분포의 위로 올라가는 지수 (a-1)과 (b-1)이 각각 "지금까지 앞면이 나온 횟수"와 "지금까지 뒷면이 나온 횟수"로 해석할 수 있다는 것이죠. 베이지안이 선험적인 지식을 인위적으로 가한다는 말이랑 연관되는 부분입니다. 이번 실험의 관측정보는 아니지만 이미 일어난 그 이전 실험의 정보를 활용해서 보정해주고 있는겁니다.
동전던지기 예시를 보면 베이지안 통계학적 관점이 아쉬운점이 하나도 없죠 ㅎㅎ.. 아귀가 딱딱맞게 업데이트되고 심지어 hyper-parameter 의미해석까지 깔끔하게 떨어지는데 사실 이런 경우는 거의 없습니다. 업데이트를 위해서는 likelihood와 prior가 conjugate의 관계(방금 Beta-Binomial처럼)에 있어야 하는데 일단 이런 pair 자체가 많지 않구요, 그렇기에 prior도 의미해석적 차원에서 결합되는 경우보다는 수학적 꼴때문에 분포가 선택되는 경우가 많아 보입니다.
conjugate prior에 대해서는 아래 위키피디아를 참고하세요
https://en.wikipedia.org/wiki/Conjugate_prior
Conjugate prior - Wikipedia
In Bayesian probability theory, if the posterior distribution p(θ | x) is in the same probability distribution family as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions, and the prior is called a
en.wikipedia.org
conjugate prior/likelihood로 모델링하기 어려운 경우 비모수적 방법을 동원하기도 합니다. MCMC방법론 등이 이 범주에 속하게 됩니다.

https://bayestour.github.io/blog/2019/07/04/npb.html
Nonparametric Bayesian 이란?
이번 포스트에서는 Nonparametric Bayesian 이 무엇인지 원리적인 부분에 대해 소개하고자 합니다. Nonparametric Bayesian 은 이름에서 볼 수 있듯이 두 통계학 용어를 섞어 놓은 분야입니다. 요약하면 Bayesia
bayestour.github.io
동전 던지기에서는 카테고리가 2개였습니다만, 카테고리 개수가 늘어날 수도 있죠? 주사위 던지기는 어떨까요? 거의 비슷한데 분포만 Dirichlet-Multinomial로 바뀔뿐입니다.

마지막으로 언급할 것이 하나 있군요. MAP와 MLE는 결국 충분한 관측치를 얻게되면 같은값으로 수렴하게 됩니다. (동전던지기에서도 처음에 5번중 앞면이 한번도 나오지 않는다면 MAP와 MLE의 괴리가 크겠지만 관측치를 더 많이 얻게되면서는 자연스럽게 문제가 많이 해결되죠?) 세부적인 사항은 아래 블로그에서 확인하세요
https://agustinus.kristia.de/techblog/2017/01/01/mle-vs-map/
MLE vs MAP: the connection between Maximum Likelihood and Maximum A Posteriori Estimation - Agustinus Kristiadi's Blog
In this post, we will see what is the difference between Maximum Likelihood Estimation (MLE) and Maximum A Posteriori (MAP).
agustinus.kristia.de
여기까지가 베이지안 통계학에 관한 기본 내용을 정리한 것입니다. 결국 핵심은 빈도주의적 관점에 "보정"을 해준다는 발상이 되겠습니다.
'Data & Research' 카테고리의 다른 글
| [Machine Learning] 모델의 평가 (0) | 2021.11.14 |
|---|---|
| [Statistics] 샘플링(Sampling)과 MCMC (0) | 2021.11.10 |
| [Statistics] 나이브 베이즈 (Naïve Bayes) (0) | 2021.11.06 |
| [Machine Learning] 앙상블(Ensemble) 기법 (1) | 2021.11.06 |
| [Machine Learning] 정보(Information) 이론 기초 (0) | 2021.11.05 |



